

La mecánica de la fractura es un área del conocimiento de la ingeniería de gran importancia. Es aplicable al estudio de propagación de grietas en materiales compuestos como el Hormigón en el cual aporta grandes conceptos a la hora de predecir el comportamiento de una estructura fisurada. En este trabajo el análisis de una viga en presencia de dos fisuras es llevado a cabo mediante modelos como el de fisura cohesiva comúnmente utilizado en materiales como el hormigón. El software Franc2d desarrollado por el grupo de Fractura de la Universidad de Cornell es utilizado en la simulación del caso de estudio.
El caso de estudio propuesto consiste de una viga de hormigón empotrada en un extremo como se muestra en la figura 1. Las dimensiones son: \(L = 4m\), \(h = 60cm\) y \(t = 15cm\). Dicha viga contiene dos grietas, una de 5cm ubicada a 30cm desde el apoyo empotrado y otra de \(20cm\) ubicada a \(2m\) del extremo.
Las propiedades mecánicas del hormigón utilizadas son: \(E=30GPa\), \(f_c = 30MPa\), \(/nu = 0,2\) y \(G_f = 80N/m\).
Para modelar de forma correcta los elementos cohesivos en la interfaz de la grieta necesitamos la resistencia a la tracción de los elementos, esta es de \(f_{ct} =4MPa\) mientras que la apertura de grieta crítica \(W_c\) se obtiene a partir de \(f_{ct}\) y \(G_f\) ya que:
\[\begin{eqnarray} G_{f} &=&\frac{1}{2}W_{c}f_{ct} \\ W_{c} &=& \frac{2G_{f}}{f_{ct}} \nonumber \\ W_{c} &=& \frac{2(80N/m)}{4MPa} \nonumber \\ W_{c}&=&40\mu m \end{eqnarray}\]Esto es suponiendo un área triangular (ablandamiento lineal).
En la figura 1 se muestra una carga \(P\) aplicada en el extremo de la viga actuando en dirección \(y\) negativo. En lugar de esto a la hora de llevar a cabo la simulación se impuso un desplazamiento al extremo de la viga, este desplazamiento fue de \(1cm\) equivaliendo el mismo a una carga aproximada \(P=32kN\).
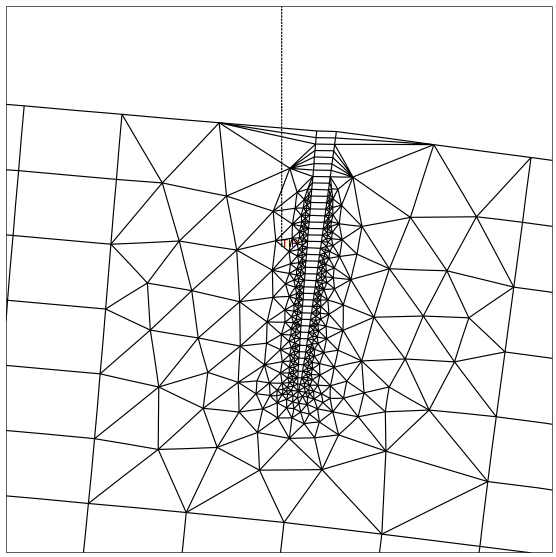
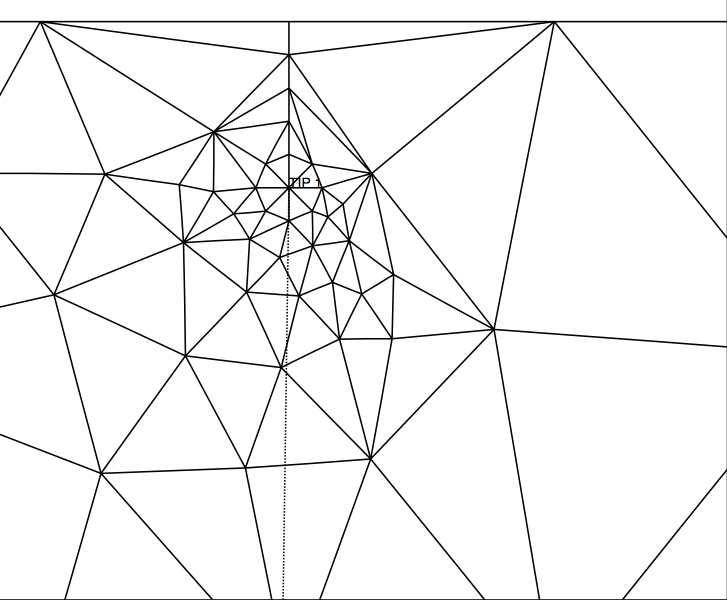
La simulación fue llevada a cabo utilizando el software Franc2d desarrollado por el grupo de fractura de la Universidad de Cornell. En primer lugar se generó el modelo y la malla de la viga utilizando el programa CASCA, una vez generado se importó a Franc2d introduciéndole las grietas, obteniendo como resultado la discretización mostrada en la figura 2. Una vista ampliada del mallado entorno a las grietas es presentado en la figura 3.
| a) Mallado - Grieta 1 | b) Mallado - Grieta 2 |
|---|---|
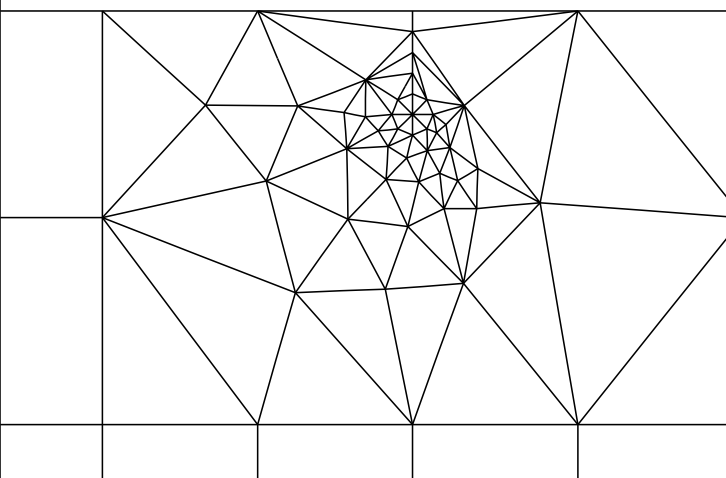 |
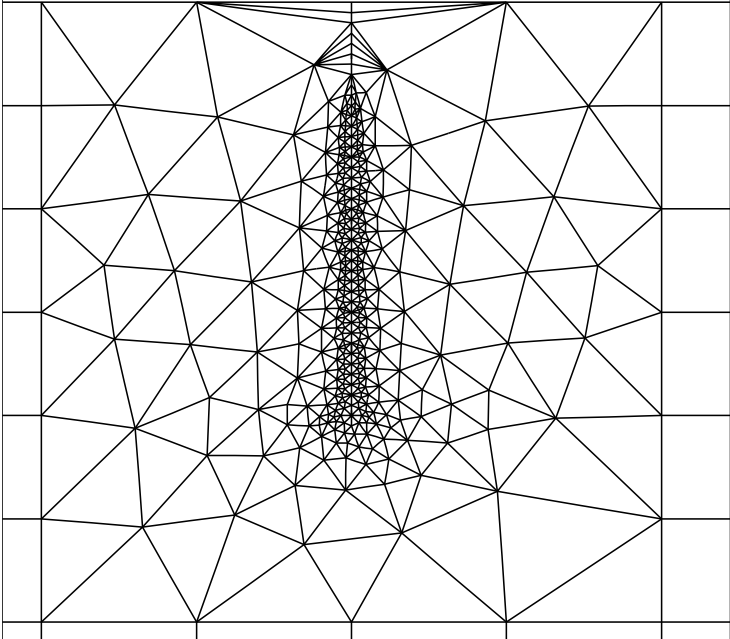 |
Fig. 3: Mallado entorno a las grietas.
Como resultado de la simulación, los resultados de la evolución de las tensiones a lo largo de los labios de la grieta así como la apertura de la misma son mostrados en la figura 1 4 para la grieta 1 y en la figura 5 para la grieta 2.
A partir de las gráficas se puede ver el comportamiento de los elementos cohesivos los cuales se ablandan progresivamente una vez alcanzan el límite de resistencia, que en este caso fue de $4MPa$, hasta un valor de cero una vez que se alcanza la longitud crítica de \(W_{c}=40\mu m\). Luego de esto los elementos no ejercen ninguna tensión sobre los labios de la grieta (ver figura 6).
| Fig. 6a | Fig. 6b |
|---|---|
 |
 |
Como resultado del análisis se pudo observar que la longitud de la zona cohesiva a lo largo de la grieta fue de \(6.12mm\) para la grieta 1 y \(3.67mm\) para la grieta 2. Esto se explica ya que al ser la grieta 2 mayor que 1, produce una concentración de tensiones mayor. Esto se puede observar en la figura sxx en la cual se muestra la evolución de las tensiones \(\sigma_{xx}\) en frente de la grieta (transversal a la sección de la viga en donde se encuentra la grieta). Para el caso de la grieta 2 la tensión en la punta de la grieta es de \(105MPa\) mientras que en la punta de la grieta 1 la tensión es de \(31.64MPa\)
Otros de los resultados obtenidos en el análisis fue la curva de ablandamiento de la zona cohesiva para las dos grietas, las mismas se presentan en las figuras 8 y 9. El área calculada numéricamente mediante el software Franc2D fue de \(72.70N/m\) y \(76.86N/m\) para la primera y segunda grieta, respectivamente.
Se realizó una predicción de propagación de las grietas de la cual se concluyó que en el caso que las grietas crezcan el fallo en el componente se produciría por una crecimiento incontrolado de la grieta 2. En la figura 10 se puede ver la dirección preferencial de propagación de la grieta mientras que en la figura 11 se ve la grieta 2 ya propagada.
| a) Dirección de propagación - Grieta 1 | b) Dirección de propagación - Grieta 2 |
|---|---|
 |
 |
| a) Propagación - Grieta 2 | b) Propagación - Grieta 2 |
|---|---|
 |
 |
Se presentaron los resultados de un análisis de fractura en una viga de hormigón utilizando el modelo de grieta cohesiva. Los resultados presentados demuestran que en caso de fallo por fisura propagante el mismo se daría en la grieta 2. También es posible ver como el valor de $G_{f}$ de las curvas cohesivas (figura 8 y 9) se aproxima de buena manera al valor teórico de $80N/m$, si se observa el valor de la grieta 2 ($76.86N/m$) es más cercano que de la grieta 1 ($72.70N/m$), esto se debe al mallado más fino realizado entorno a la grieta 2.
1: El eje Depth en las figuras 4 y 5 representa una distancia relativa desde un punto a lo largo de la longitud de la fisura y la punta de la fisura propiamente dicha.↩
